Capital Budgeting problems
A collection of capital budgeting problems with solutions.

Here is a collection of capital budgeting problems with their solutions. This is the notation used throughout the post:
\begin{array}{c|l} \textbf{Symbol} & \textbf{Description} \\ \hline P & \text{Price of an asset} \\ r & \text{Discount rate per period} \\ N & \text{Number of periods } \\ t & \text{Current period in tables and summations} \\ CF_t & \text{Cashflow at period }t \\ I_0 & \text{Initial investment, }CF_0 = -I_0 \\ \hline \end{array}And a summary of formulas:
\begin{aligned} & \sum_{t=0}^{payback} CF_t = 0 \textcolor{red}{\longrightarrow} \sum_{t=1}^{payback} CF_t = I_0 \\ \\ & \sum_{t=0}^{payback} \textcolor{red}{\underbrace{\textcolor{black}{\frac{CF_t}{\left(1+r \right)^t}}}_{{PV_t}}} = 0 \textcolor{red}{\longrightarrow} \sum_{t=1}^{payback} \frac{CF_t}{(1+r)^t} = I_0 \\ \\ & NPV = \sum_{t=0}^N \textcolor{red}{\underbrace{\textcolor{black}{\frac{CF_t}{\left(1+r \right)^t}}}_{{PV_t}}} = -I_0 + \sum_{t=1}^N \frac{CF_t}{(1+r)^t} \\ \\ & \sum_{t=0}^{N} \frac{CF_t}{(1 + IRR)^t} = 0 \textcolor{red}{\longrightarrow} r = IRR \Rightarrow NPV=0 \\ \\ & \text{Profitability Index} = \frac{ \displaystyle \sum_{t=1}^N \frac{CF_t}{(1+r)^t}}{I_0} \\ \end{aligned}Problem 1
What is the payback period for this investment?
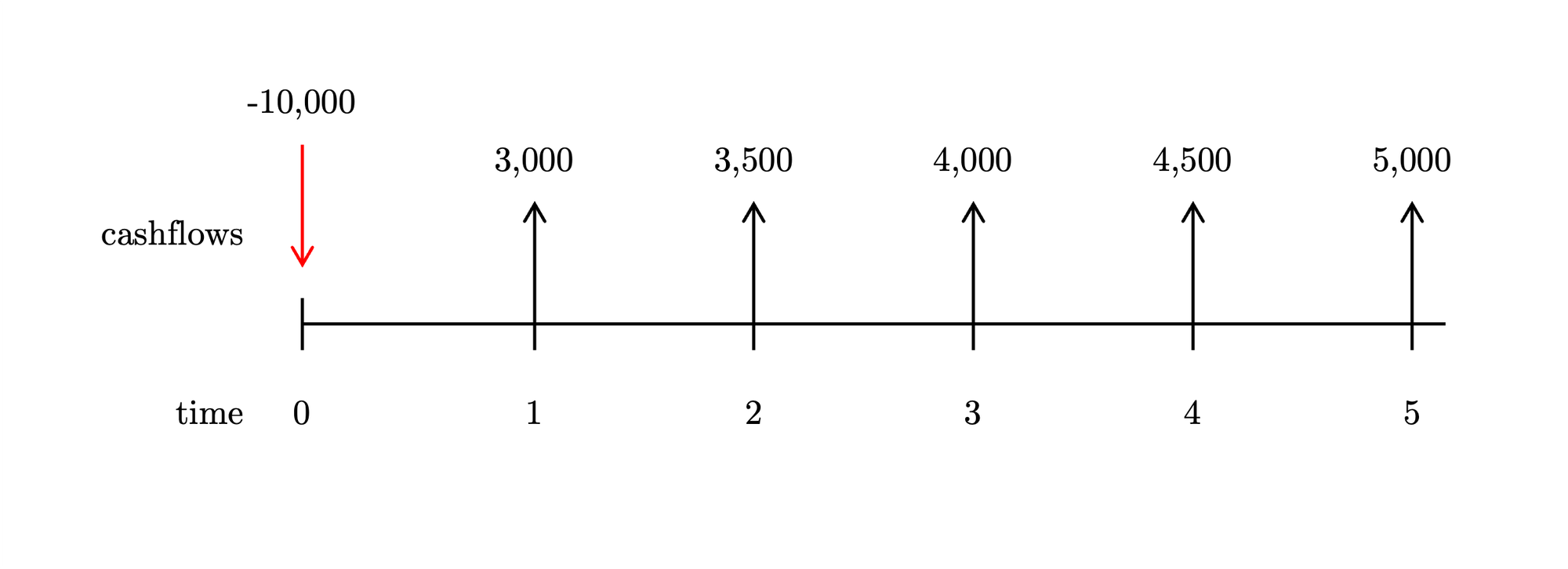
Let's accumulate the cash flows until the sum is equal or greater than the initial investment. The payback period is the year when that condition is first met:
\begin{aligned} & \sum_{t=1}^{\textcolor{red}{payback}} CF_{t} = I_0 \\ \\ & CF_1 + CF_2 + CF_\textcolor{red}{3} \ge I_0 \\ \\ & \$3,000 + \$3,500 + \$4,000 \ge \$ 10,000 \\ \end{aligned}In the following table, the payback period is the row where the cumulative amount first reaches zero or turns positive:
\begin{array}{rrr} \hline t & CF_t & \sum{CF_t} \\ \hline 0 & -10000 & -10000 \\ 1 & 3000 & -7000 \\ 2 & 3500 & -3500 \\ \textcolor{red}{3} & 4000 & \textcolor{red}{+500} \\ 4 & 4500 & \cdots \\ 5 & 5000 & \cdots \end{array}Answer
The payback period is 3 years. By the end of the third year, the project has generated enough cash flows to cover the initial investment.
Problem 2
What is the discounted payback period for this investment if the discount rate is 10%?
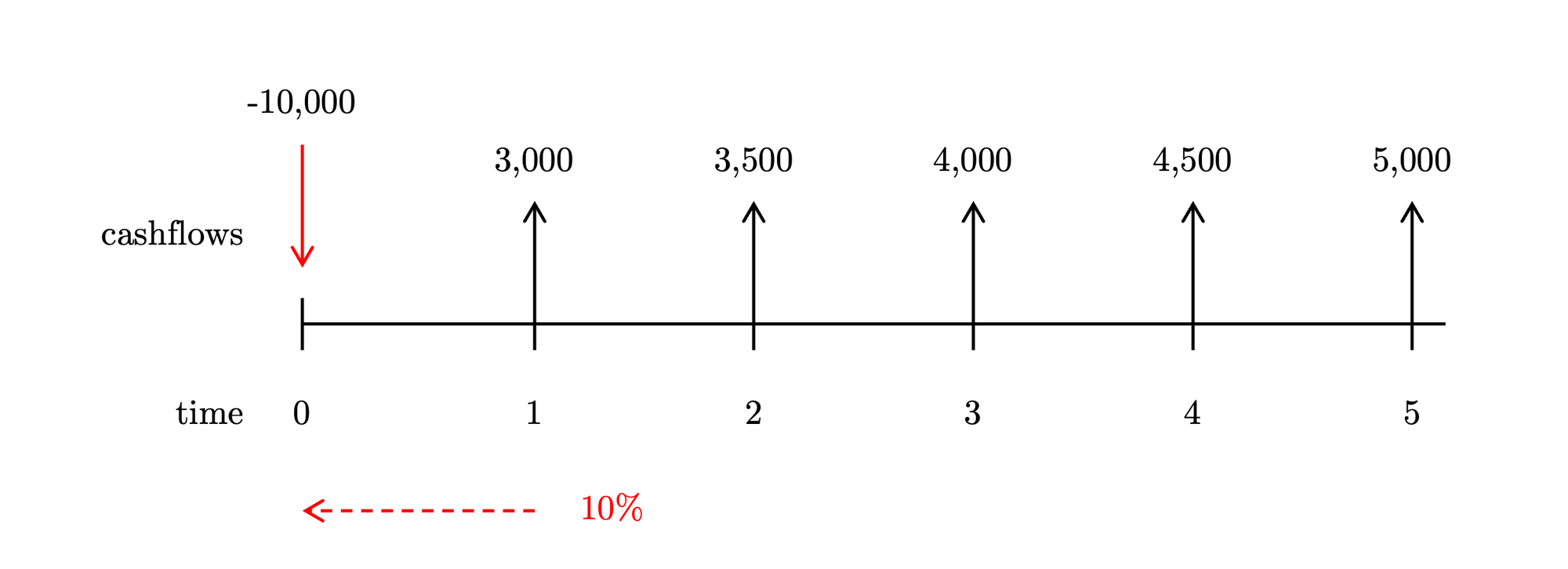
Let's accumulate the present value of the cashflows until the sum is equal or greater than the initial investment. The discounted payback period is the year when that condition is first met:
\begin{aligned} & \sum_{t=1}^{\textcolor{red}{payback}} \frac{CF_t}{(1+r)^t} = I_0 \\ \\ & \frac{CF_1}{1+r} + \frac{CF_2}{(1+r)^2} + \frac{CF_3}{(1+r)^3} + \frac{CF_\textcolor{red}{4}}{(1+r)^\textcolor{red}{4}} \ge I_0 \\ \\ & \textcolor{red}{\underbrace{\textcolor{black}{\frac{3000}{1+0.1}}}_{PV_1}} + \textcolor{red}{\underbrace{\textcolor{black}{\frac{3500}{(1+0.1)^2}}}_{PV_2}} + \textcolor{red}{\underbrace{\textcolor{black}{\frac{4000}{(1+0.1)^3}}}_{PV_3}} + \textcolor{red}{\underbrace{\textcolor{black}{\frac{4500}{(1+0.1)^\textcolor{red}{4}}}}_{PV_4}} \ge 10000 \\ \end{aligned}In the following table, the payback period is the row where the cumulative amount first reaches zero or turns positive:
\begin{array}{rrrr} \hline t & CF_t & PV_t & \sum{PV_t} \\ \hline 0 & -10000 & -10000 & -10000\\ 1 & 3000 & 2727.27 & -7272.73 \\ 2 & 3500 & 2892.56 & -4380.17 \\ 3 & 4000 & 3005.26 & -1374.91 \\ \textcolor{red}{4} & 4500 & 3073.56 & \textcolor{red}{+1698.65} \\ 5 & 5000 & \cdots & \cdots \\ \end{array}Answer
The discounted payback period is 4 years. By the end of the fourth year, the project has generated enough cash flows to cover the initial investment with their present value.
Problem 3
If the company’s required rate of return is 10%, should it proceed with the investment?
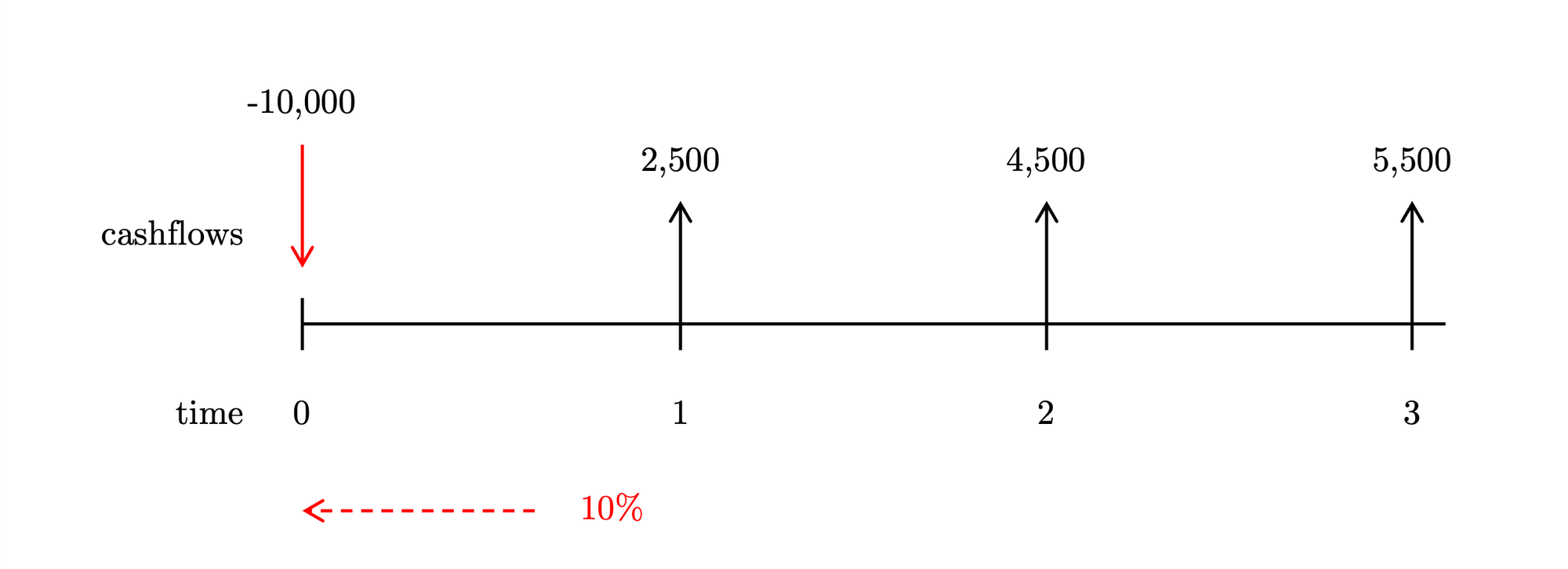
Let's calculate the NPV, this is the formula:
\begin{align} NPV & = \sum_{t=0}^T \frac{CF_t}{\left( 1+r \right)^t} = -I_0 + \sum_{t=1}^T PV_t \\ \\ NPV &= -10000 + \textcolor{red}{\underbrace{\textcolor{black}{\frac{2500}{\left( 1 + 0.1 \right)^1}}}_{PV_1}} + \textcolor{red}{\underbrace{\textcolor{black}{\frac{4500}{\left( 1 + 0.1 \right)^2}}}_{PV_2}} + \textcolor{red}{\underbrace{\textcolor{black}{\frac{5500}{\left( 1 + 0.1 \right)^3}}}_{PV_3}} = \$ \textbf{538.92} \end{align}The calculations shown in a table:
\begin{array}{rrr} \hline t & CF_t & PV_t \\ \hline 0 & -10000 & -10000.00 \\ 1 & 2500 & 2314.81 \\ 2 & 4500 & 3858.0.2 \\ 3 & 5500 & 4366.08 \\ \hline & & \$ \textbf{538.92} \end{array}Answer
The project should be accepted because its \(NPV \ge 0\), indicating that the investment meets or exceeds the required rate of return.
Problem 4
If the company’s required rate of return is 8%, should it proceed with the investment?
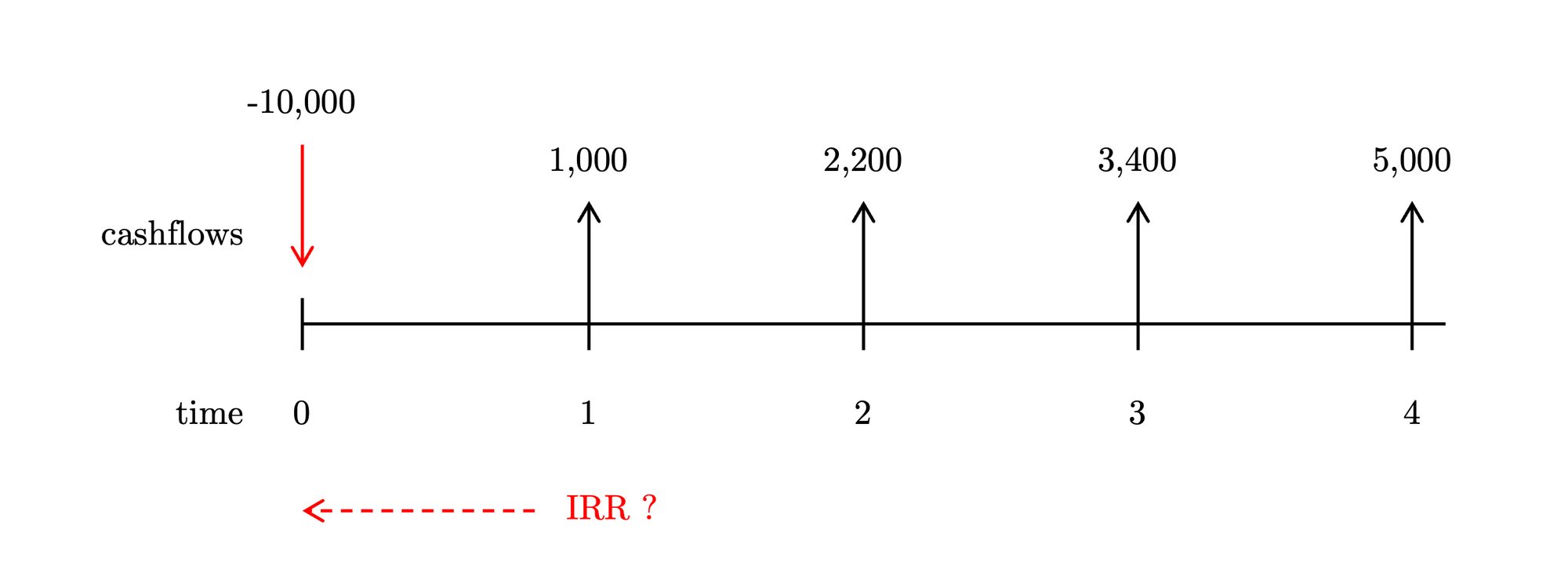
Let's calculate the Internal Rate of Return (IRR):
\begin{aligned} & \sum_{t=0}^{N} \frac{CF_t}{(1 + IRR)^t} = 0 \textcolor{red}{\longrightarrow} r = IRR \Rightarrow NPV=0 \\ \\ & -10000 + \frac{1000}{1 + \textcolor{red}{IRR}} + \frac{2200}{(1 + \textcolor{red}{IRR})^2} + \frac{3400}{(1 + \textcolor{red}{IRR})^3} + \frac{5000}{(1 + \textcolor{red}{IRR})^4} = 0 \end{aligned}Which yields an IRR of 5%.
Answer
Since 5% is less than the required rate of return (8%), the company should reject the project.





