Bond Valuation Problems
A collection of bond valuation problems with solutions.
Here is a collection of bond valuation problems with their solutions. This is the notation used in this post:
\begin{array}{c|l} \textbf{Symbol} & \textbf{Description} \\ \hline P & \text{Price of the bond} \\ F & \text{Face value (also Par value)} \\ T & \text{Number of years to maturity} \\ c & \text{Annual coupon rate} \\ m & \text{Number of payments per year} \\ y & \text{Yield to Maturity, market interest rate per year} \\ \hline C & \text{Coupon payment per period, } \textstyle{C=F \cdot \frac{c}{m}}\\ r & \text{Discount rate per period, } \textstyle{r=\frac{y}{m}} \\ N & \text{Number of periods, } N = T \cdot m \\ t & \text{Current period in tables and summations} \\ CF_t & \text{Cashflow at period }t \\ \hline \mathcal{D} & \text{Macaulay duration} \\ \mathcal{D}^* & \text{Modified duration} \\ \mathcal{C} & \text{Convexity} \\ \hline \end{array}And a summary of formulas:
\begin{aligned} & P = \sum_{t=1}^N \textcolor{red}{\underbrace{\textcolor{black}{\frac{CF_t}{\left(1+r \right)^t}}}_{{PV_t}}} = \textcolor{red}{\underbrace{\textcolor{black}{C \cdot \left[ \frac{1 - \left( 1 + r \right) ^{-N}}{r} \right]}}_{\text{PV(annuity)}}} + \textcolor{red}{\underbrace{\textcolor{black}{\frac{F}{\left( 1 + r\right)^N}}}_{\text{PV(F)}}} \\ \\ & \mathcal{D}= \frac{1}{Pm} \sum_{t=1}^N \textcolor{red}{\underbrace{\textcolor{black}{\frac{CF_t}{\left(1+r \right)^t}}}_{{PV_t}}} \cdot t \\ \\ & \mathcal{D}^*= - \frac{1}{P} \frac{\partial P}{\partial y} \quad \textcolor{red}{\longrightarrow} \quad \mathcal{D}^* = \frac{\mathcal{D}}{1+r} = \frac{1}{P m (1+r)} \sum_{t=1}^N \textcolor{red}{\underbrace{\textcolor{black}{\frac{CF_t}{\left(1+r \right)^t}}}_{{PV_t}}} \cdot t \\ \\ & \mathcal{C} = \frac{1}{P} \frac{\partial^2 P}{\partial^2 y} \quad \textcolor{red}{\longrightarrow} \quad \mathcal{C} = \frac{1}{P m^2 (1+r)^2} \sum_{t=1}^{N} \textcolor{red}{\underbrace{\textcolor{black}{\frac{CF_t}{\left(1+r \right)^t}}}_{{PV_t}}} \cdot t \cdot (t+1) \\ \\ & \frac{\Delta P}{P} \approx - \mathcal{D}^* \cdot \Delta y + \frac{\mathcal{C}}{2} \cdot \left( \Delta y \right)^2 \end{aligned}Problem 1
✏️
Find the value of a 10-year zero-coupon bond with a $1,000 par value and a YTM of 5%.
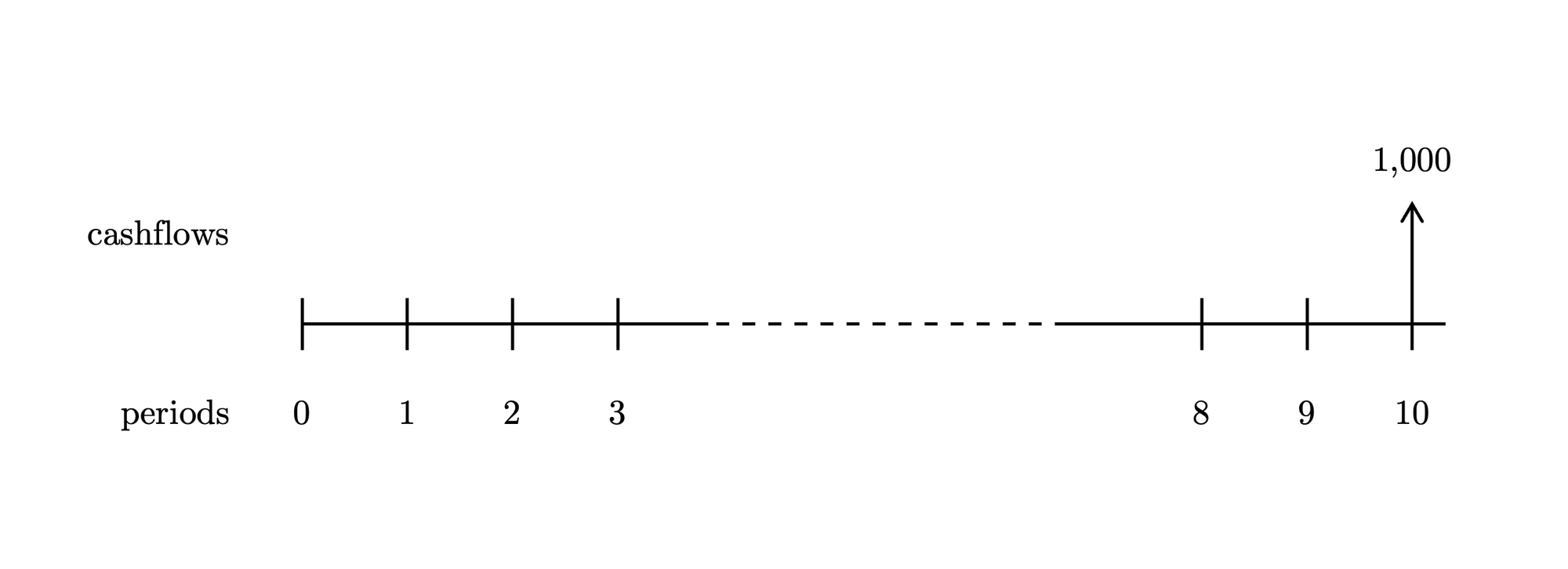
Answer
The price is \( \$ \textbf{613.91} \).
Problem 2
✏️
A company issues a bond with a face value of $1,000 and 5 years remaining until maturity. The bond pays interest annually and carries a coupon rate of 6%. If the discount rate is 7%, what is the price of this bond?
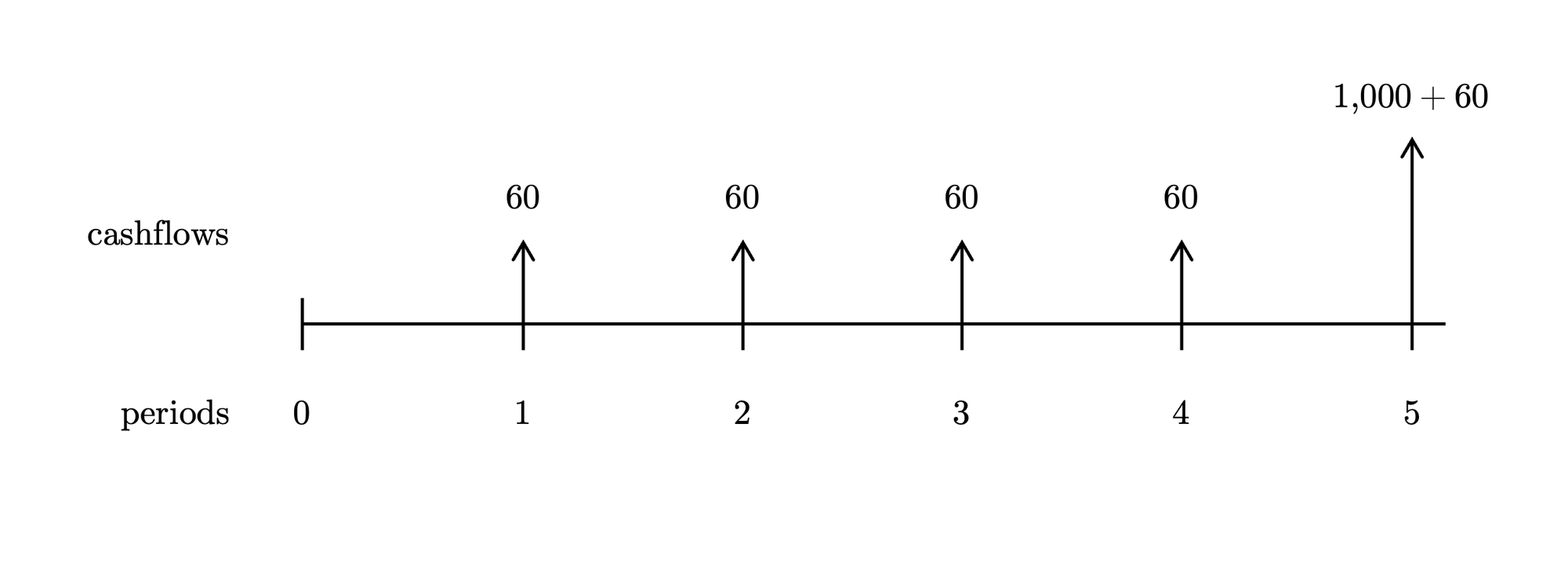
The calculations shown in a table:
\begin{array}{rrr} \hline t & CF_t & PV_t \\ \hline 1 & 60 & 56.07 \\ 2 & 60 & 52.41 \\ 3 & 60 & 48.98 \\ 4 & 60 & 45.77 \\ 5 & 1060 & 755.77 \\ \hline & & \textbf{959.00} \end{array}Answer
The price is \( \$ \textbf{959.00} \).
Problem 3
✏️
A company issues a bond with a face value of $1,000 and 3 years remaining until maturity. The bond pays interest semiannually and carries a coupon rate of 8%. If the discount rate is 6%, what is the price of this bond?
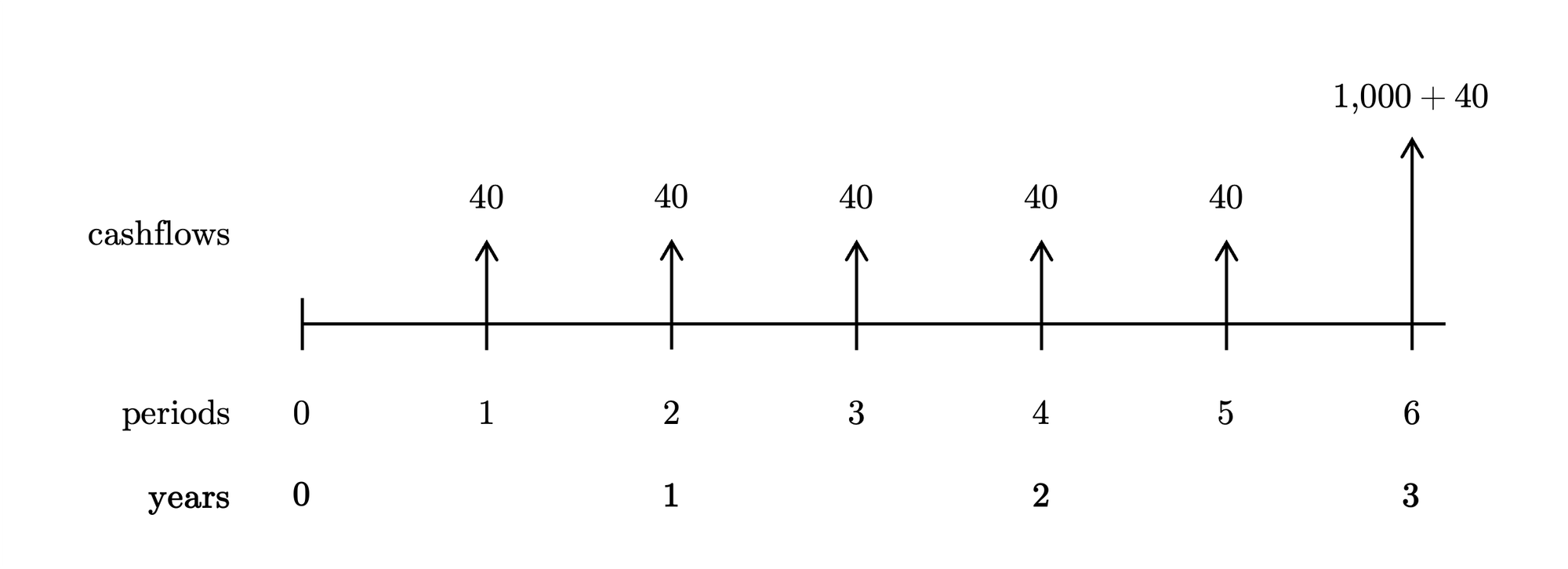
The calculations shown in a table:
\begin{array}{rrrr} \hline t & t/m & CF_t & PV_t \\ \hline 1 & 0.5 & 40 & 38.83 \\ 2 & 1.0 & 40 & 37.70 \\ 3 & 1.5 & 40 & 36.61 \\ 4 & 2.0 & 40 & 35.54 \\ 5 & 2.5 & 40 & 34.50 \\ 6 & 3.0 & 1040 & 870.98 \\ \hline & & & \textbf{1054.17} \end{array}Answer
The price is \( \$ \textbf{1054.17} \).
Problem 4
✏️
A $1,000 bond matures in 30 months, pays interest semiannually, and carries an annual coupon rate of 9%.
- What is the price of this bond if the discount rate is 6%?
- Calculate Macaulay, modified duration, and convexity.
- What will be the new bond price if interest rates increase by 1%?
- What is the price of this bond if the discount rate is 6%?
- Calculate Macaulay, modified duration, and convexity.
- What will be the new bond price if interest rates increase by 1%?
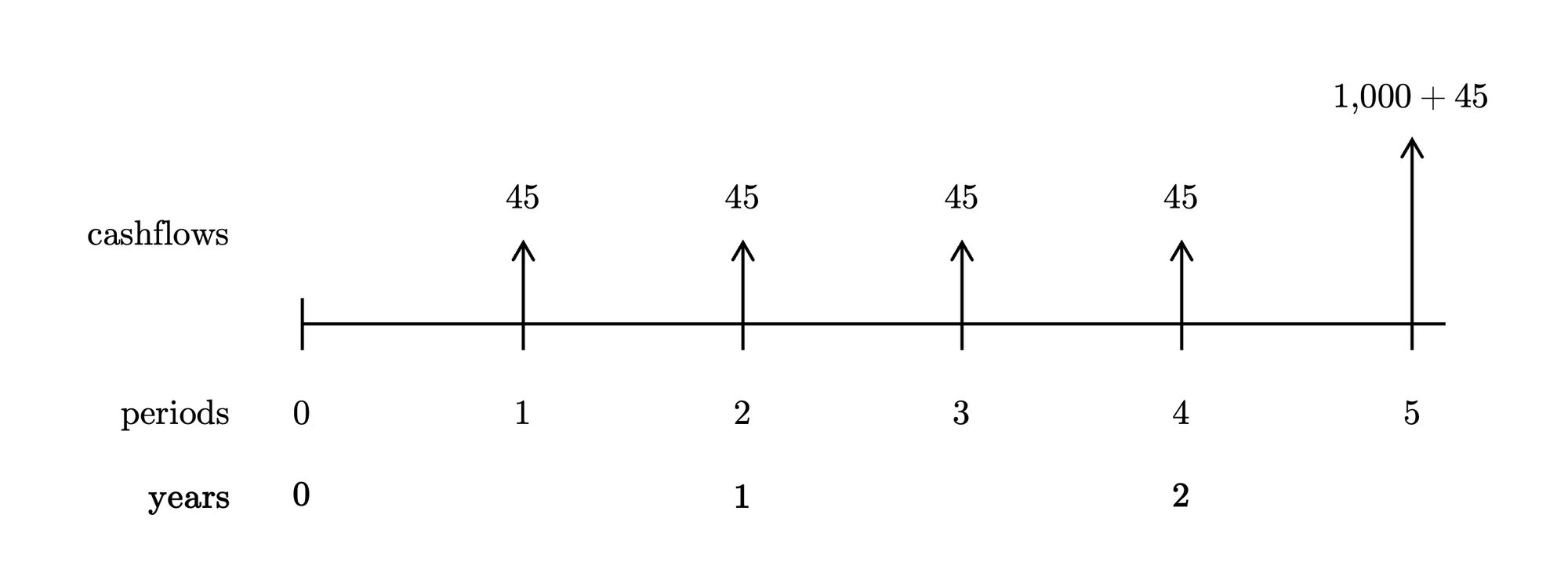
The calculations shown in a table:
\begin{array}{rrrr} \hline t & t/m & CF_t & PV_t & t \cdot PV_t & t \cdot (t+1) \cdot PV_t \\ \hline 1 & 0.5 & 45 & 43.69 & 43.69 & 87.38 \\ 2 & 1.0 & 45 & 42.42 & 84.83 & 254.50 \\ 3 & 1.5 & 45 & 41.18 & 123.54 & 494.18 \\ 4 & 2.0 & 45 & 39.98 & 159.93 & 799.64 \\ 5 & 2.5 & 1045 & 901.43 & 4507.13 & 27042.79 \\ \hline & & & \textbf{1068.70} & \textbf{4919.13} & \textbf{28678.48} \\ \end{array}Answer
The bond price is \( \$ \textbf{1068.70} \), macaulay duration is \( \mathcal{D}=\textbf{2.301} \) years, modified duration is \( \mathcal{D}^*=\textbf{2.234}\), convexity is \( \mathcal{C}=\textbf{6.324} \) and the price will decrease by \(\textbf{2.20}\%\) if interest rates increase by \(\Delta y=1\%\).
